空间变换库对比与动机

引言：空间变换的普遍需求与实现困境

结论：常见库在“裁剪 ROI → 重采样 → 分析 → 回传”的标准流程中，易出现坐标偏移、配置冗余与轴序混乱；SpaceTransformer 以声明式空间定义与统一变换接口，显著降低实现复杂度并保持精度。

在医学图像分析流水线中，空间变换是一个核心且不可避免的环节。典型的工作流程包括：提取感兴趣区域（ROI）、重采样到标准尺寸、执行AI分析、将结果精确映射回原始图像空间。这一流程看似简单，但在实际实现中却充满了技术陷阱。

本文通过一个具体对比实验，展示主流库在该流程中的问题，并介绍 SpaceTransformer 如何以统一设计解决这些挑战。

测试场景设计

为了客观评估不同库的表现，我们设计了一个简化但具有代表性的测试场景：

import numpy as np
import matplotlib.pyplot as plt

def create_test_image():
    """
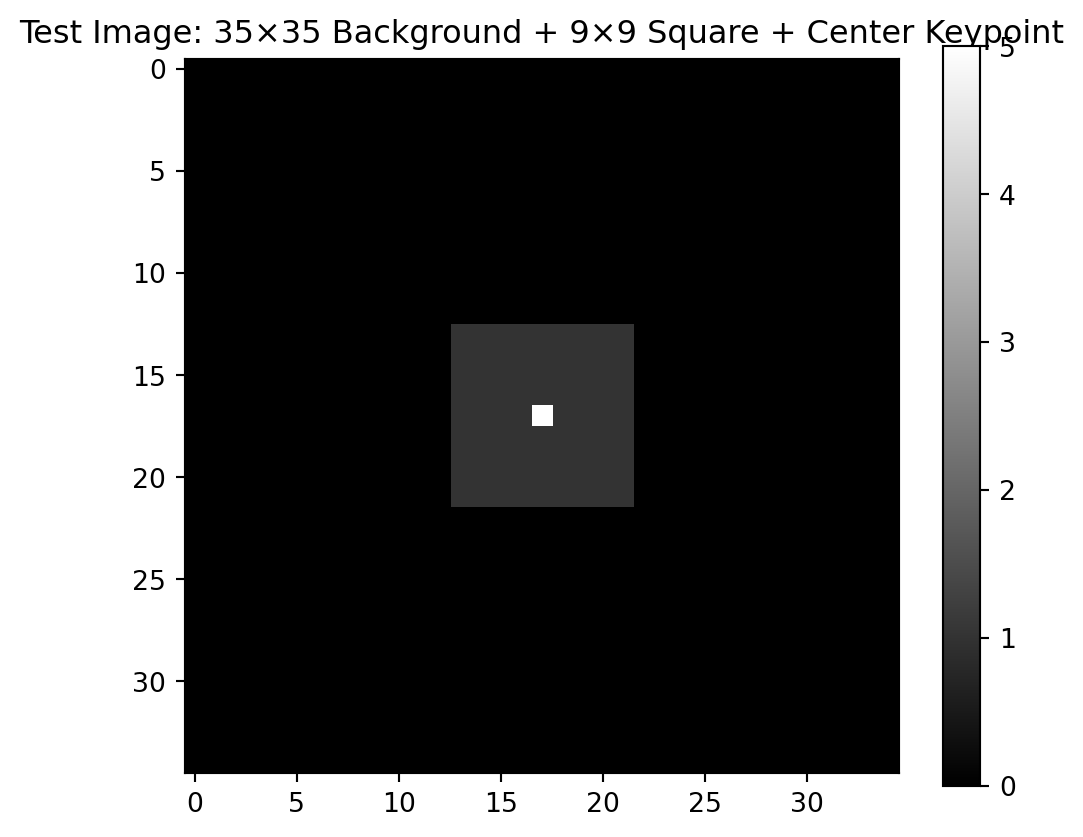
    创建测试图像：35×35 背景 + 9×9 中心正方形 + 中心关键点
    这个设计模拟了医学图像中的典型结构：器官边界 + 内部标志点
    """
    img = np.zeros((35, 35), dtype=np.float32)
    
    # 9x9正方形物体（模拟器官）
    center = 35 // 2
    half_size = 4  # 9x9的一半
    img[center-half_size:center+half_size+1, center-half_size:center+half_size+1] = 1.0
    
    # 中心关键点（模拟需要定位的解剖标志）
    img[center, center] = 5
    
    return img

def get_segmentation(img, threshold=0.5):
    """提取分割掩膜"""
    return (img >= threshold).astype(np.uint8)

def get_keypoint(img):
    """检测关键点：输出(x,y)格式的2D点"""
    candidates = np.array(np.where(img >= 3))
    if candidates.size > 0:
        # 返回(y,x)格式的点坐标
        center_y = candidates[0].mean()
        center_x = candidates[1].mean()
        return np.array([center_y, center_x])
    else:
        return np.array([0.0, 0.0])

# === 全局参数配置 ===
# ROI 提取参数（偏移的 bbox，模拟实际检测中的偏移）
ROI_START_Y = 10
ROI_START_X = 10
ROI_SIZE = 15
ROI_END_Y = ROI_START_Y + ROI_SIZE  # 25
ROI_END_X = ROI_START_X + ROI_SIZE  # 25

# 重采样目标尺寸
TARGET_SIZE = 32

# 创建测试数据
original_img = create_test_image()
original_shape = original_img.shape

print(f"原始图像尺寸: {original_shape}")
print(f"目标物体覆盖范围: {np.argwhere(original_img > 0.5).min(axis=0)} 到 {np.argwhere(original_img > 0.5).max(axis=0)}")
print(f"ROI区域: ({ROI_START_Y}:{ROI_END_Y}, {ROI_START_X}:{ROI_END_X})")
print(f"目标尺寸: {TARGET_SIZE}x{TARGET_SIZE}")

# 计算真实关键点位置（理论值）
true_keypoint = np.array([17, 17])  # 35x35图像的中心 (y, x)

def plot_result(original_img, segment_result, keypoint_result, method_name, true_keypoint):
    """统一的结果绘制函数"""
    plt.figure(figsize=(8, 6))
    plt.imshow(original_img, cmap='gray', alpha=0.7)
    if segment_result is not None:
        plt.contour(segment_result, levels=[0.5], colors='red', linewidths=2)
    
    # 显示检测到的关键点
    if keypoint_result is not None and len(keypoint_result) > 0:
        if keypoint_result.ndim == 1:  # SpaceTransformer返回的是1D数组
            plt.plot(keypoint_result[1], keypoint_result[0], 'ro', markersize=8, label='Detected Point')
        else:  # 其他方法可能返回2D数组
            plt.plot(keypoint_result[0, 1], keypoint_result[0, 0], 'ro', markersize=8, label='Detected Point')
    
    # 显示真实关键点
    plt.plot(true_keypoint[1], true_keypoint[0], 'g+', markersize=12, 
           markeredgewidth=3, label='Ground Truth')
    
    plt.title(f'{method_name} Result')
    plt.legend()
    plt.grid(True, alpha=0.3)
    
    # 计算坐标误差
    if keypoint_result is not None and len(keypoint_result) > 0:
        if keypoint_result.ndim == 1:
            error = np.linalg.norm(keypoint_result - true_keypoint)
        else:
            error = np.linalg.norm(keypoint_result[0] - true_keypoint)
        plt.text(0.02, 0.98, f'Error: {error:.3f} pixels', transform=plt.gca().transAxes, 
                bbox=dict(boxstyle='round', facecolor='white', alpha=0.8), verticalalignment='top')
    
    plt.tight_layout()
    plt.show()

plt.figure(figsize=(6, 5))
plt.imshow(original_img, cmap='gray')
plt.title('Test Image: 35×35 Background + 9×9 Square + Center Keypoint')
plt.colorbar()
plt.show()

测试流水线定义

我们将实现以下标准的医学图像处理流水线：

1. ROI 提取：从 35×35 图像中提取 15×15 中心区域
2. 重采样：将 15×15 区域缩放到 32×32
3. 分析处理：执行分割与关键点检测
4. 结果回传：将 32×32 空间结果精确映射回 35×35 原始空间

每个库的实现将被评估其代码复杂度、参数管理难度以及坐标变换的准确性。

方法一：SimpleITK 实现

SimpleITK是医学图像处理的标准库，提供了完整的ITK功能接口。

import SimpleITK as sitk

def process_with_simpleitk(img):
    """使用 SimpleITK 实现完整流水线"""
    
    # 转换为 SimpleITK 图像
    sitk_img = sitk.GetImageFromArray(img)
    sitk_img.SetSpacing([1.0, 1.0])
    sitk_img.SetOrigin([0.0, 0.0])
    
    # 步骤 1：ROI 提取（使用全局参数）
    original_size = sitk_img.GetSize()
    roi_size = [ROI_SIZE, ROI_SIZE] 
    roi_start = [ROI_START_X, ROI_START_Y]  # 注意 SimpleITK 使用 (X,Y) 顺序
    
    roi_img = sitk.RegionOfInterest(sitk_img, roi_size, roi_start)
    
    # 步骤 2：重采样到目标尺寸
    target_size = [TARGET_SIZE, TARGET_SIZE]
    
    # 计算新的spacing以保持物理尺寸
    original_spacing = roi_img.GetSpacing()
    physical_size = [roi_size[i] * original_spacing[i] for i in range(2)]
    target_spacing = [physical_size[i] / target_size[i] for i in range(2)]
    
    # 配置重采样器
    resampler = sitk.ResampleImageFilter()
    resampler.SetOutputSpacing(target_spacing)
    resampler.SetSize(target_size)
    resampler.SetOutputOrigin(roi_img.GetOrigin())
    resampler.SetOutputDirection(roi_img.GetDirection())
    resampler.SetInterpolator(sitk.sitkLinear)
    resampler.SetDefaultPixelValue(0)
    
    resampled_img = resampler.Execute(roi_img)
    resampled_array = sitk.GetArrayFromImage(resampled_img)
    
    # 步骤 3：分析处理
    segment_result = get_segmentation(resampled_array)
    keypoint_result = get_keypoint(resampled_array)
    
    # 步骤 4：结果回传 - 这里是 SimpleITK 的复杂之处
    # 需要手动计算多个坐标变换
    
    # 4a: 从目标尺寸回到ROI空间
    scale_factor = np.array(roi_size) / np.array(target_size)
    keypoint_in_roi = keypoint_result * scale_factor
    
    # 4b: 从ROI空间回到原始空间
    keypoint_in_original = keypoint_in_roi + np.array([roi_start[1], roi_start[0]])
    
    # 分割结果回传需要再次重采样
    segment_sitk = sitk.GetImageFromArray(segment_result.astype(np.float32))
    segment_sitk.SetSpacing(target_spacing)
    segment_sitk.SetOrigin(resampled_img.GetOrigin())
    
    # 重采样回 ROI 尺寸
    back_resampler = sitk.ResampleImageFilter()
    back_resampler.SetOutputSpacing(original_spacing)
    back_resampler.SetSize(roi_size)
    back_resampler.SetOutputOrigin(roi_img.GetOrigin())
    back_resampler.SetInterpolator(sitk.sitkNearestNeighbor)
    back_resampler.SetDefaultPixelValue(0)
    
    segment_roi = back_resampler.Execute(segment_sitk)
    segment_roi_array = sitk.GetArrayFromImage(segment_roi)
    
    # 将ROI结果放回原始图像
    segment_original = np.zeros(original_shape, dtype=np.uint8)
    segment_original[roi_start[1]:roi_start[1]+roi_size[1], 
                    roi_start[0]:roi_start[0]+roi_size[0]] = segment_roi_array
    
    return segment_original, keypoint_in_original

print("=== SimpleITK实现 ===")
sitk_segment, sitk_keypoint = process_with_simpleitk(original_img)
print(f"检测到的关键点坐标: {sitk_keypoint}")
print(f"分割区域像素数: {np.sum(sitk_segment)}")

# 立即显示 SimpleITK 结果
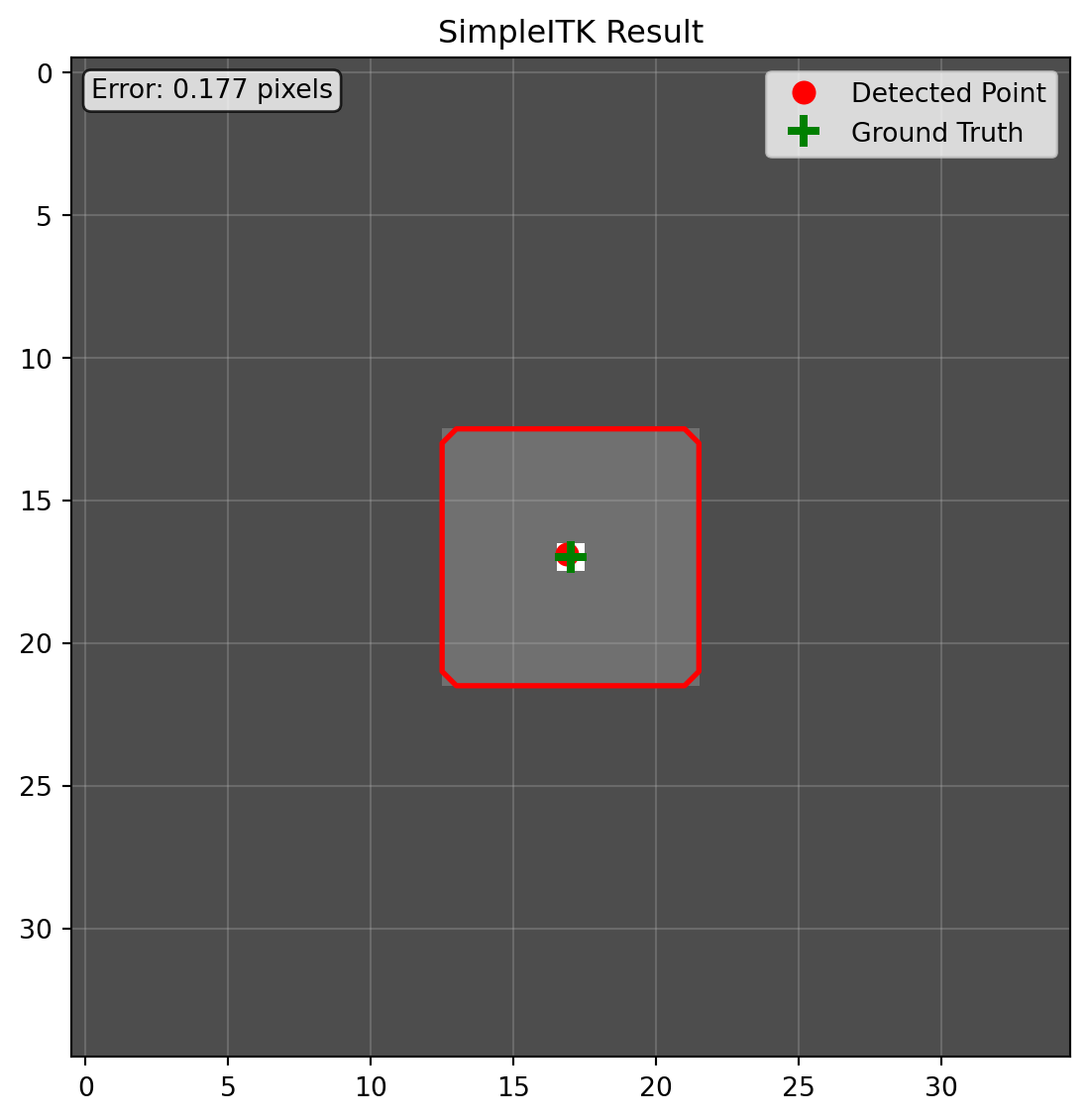
plot_result(original_img, sitk_segment, sitk_keypoint, "SimpleITK", true_keypoint)

SimpleITK 的问题分析：

• 重采样配置冗长：每次重采样都需要配置多个参数
• 代码可读性差：业务逻辑被大量底层配置代码掩盖
• 轴序问题：这张图xy对称，所以体现不出来，但实际上很容易出现轴序错误

方法二：scipy.ndimage 实现

scipy.ndimage是通用的N维图像处理库，在科学计算社区广泛使用。

from scipy import ndimage
from scipy.ndimage import zoom

def process_with_scipy(img):
    """使用 scipy.ndimage 实现流水线"""
    
    # 步骤 1：ROI 提取（使用全局参数）
    h, w = img.shape
    roi_img = img[ROI_START_Y:ROI_END_Y, ROI_START_X:ROI_END_X]
    
    # 步骤 2：重采样到目标尺寸
    zoom_factor = TARGET_SIZE / ROI_SIZE
    
    # 注意：scipy的zoom函数坐标处理容易出错
    resampled_img = zoom(roi_img, zoom_factor, order=1, mode='constant', cval=0)
    
    # 步骤 3：分析处理
    segment_result = get_segmentation(resampled_img)
    keypoint_result = get_keypoint(resampled_img)
    
    # 步骤 4：结果回传
    # 4a: 关键点坐标变换
    keypoint_in_roi = keypoint_result / zoom_factor
    keypoint_in_original = keypoint_in_roi + [ROI_START_Y, ROI_START_X]
    
    # 4b: 分割结果回传
    # zoom函数的逆变换参数计算容易出错
    segment_roi = zoom(segment_result.astype(np.float32), 
                      1.0 / zoom_factor, order=0, mode='constant', cval=0)
        
    # 放回原始图像
    segment_original = np.zeros_like(img, dtype=np.uint8)
    segment_original[ROI_START_Y:ROI_END_Y, ROI_START_X:ROI_END_X] = segment_roi
    
    return segment_original, keypoint_in_original

print("=== scipy.ndimage实现 ===")
scipy_segment, scipy_keypoint = process_with_scipy(original_img)
print(f"检测到的关键点坐标: {scipy_keypoint}")
print(f"分割区域像素数: {np.sum(scipy_segment)}")

# 立即显示 scipy.ndimage 结果
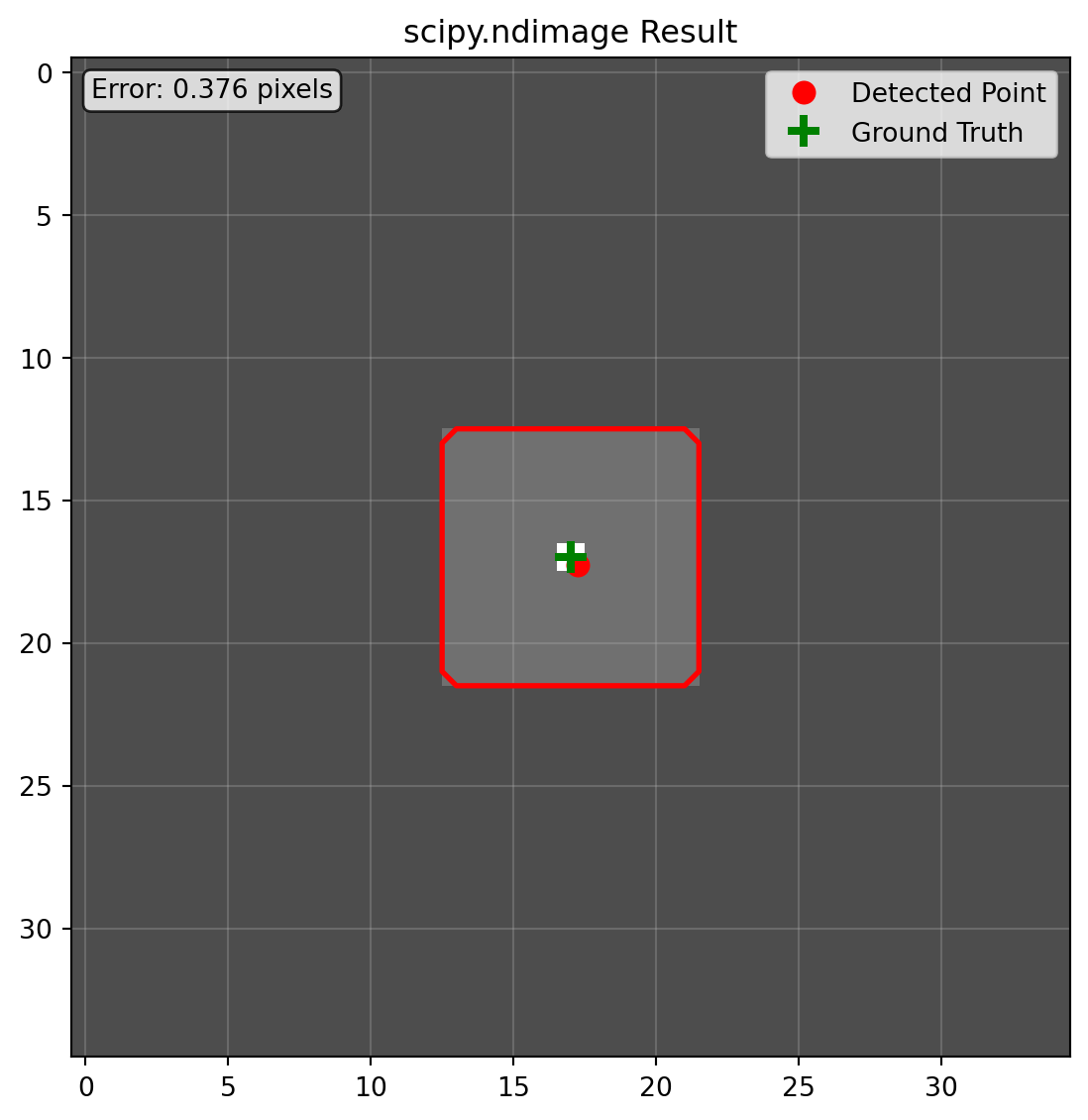
plot_result(original_img, scipy_segment, scipy_keypoint, "scipy.ndimage", true_keypoint)

scipy.ndimage 的问题分析： - zoom函数：逆变换时尺寸计算容易出现舍入误差

方法三：PyTorch interpolate 实现

PyTorch的functional.interpolate是深度学习中最常用的图像变换工具。

import torch
import torch.nn.functional as F

def process_with_pytorch(img):
    """使用 PyTorch interpolate 实现流水线"""
    
    # 转换为 PyTorch 张量（需要添加 batch 与 channel 维度）
    tensor_img = torch.from_numpy(img).unsqueeze(0).unsqueeze(0).float()
    
    # 步骤 1：ROI 提取（使用全局参数）
    h, w = img.shape
    roi_tensor = tensor_img[:, :, ROI_START_Y:ROI_END_Y, ROI_START_X:ROI_END_X]
    
    # 步骤 2：重采样到目标尺寸
    
    # PyTorch的align_corners参数经常导致混淆
    resampled_tensor = F.interpolate(roi_tensor, size=(TARGET_SIZE, TARGET_SIZE), 
                                   mode='bilinear', align_corners=False)
    
    resampled_img = resampled_tensor.squeeze().numpy()
    
    # 步骤 3：分析处理
    segment_result = get_segmentation(resampled_img)
    keypoint_result = get_keypoint(resampled_img)
    
    # 步骤 4：结果回传
    # PyTorch的坐标变换计算复杂，align_corners设置影响结果
    scale_factor = ROI_SIZE / TARGET_SIZE
    
    keypoint_in_original = keypoint_result * scale_factor + [ROI_START_Y, ROI_START_X]
    
    # 分割结果回传
    segment_tensor = torch.from_numpy(segment_result.astype(np.float32)).unsqueeze(0).unsqueeze(0)
    segment_roi_tensor = F.interpolate(segment_tensor, size=(ROI_SIZE, ROI_SIZE), 
                                     mode='nearest')
    
    segment_roi = segment_roi_tensor.squeeze().numpy().astype(np.uint8)
    
    # 放回原始图像
    segment_original = np.zeros_like(img, dtype=np.uint8)
    segment_original[ROI_START_Y:ROI_END_Y, ROI_START_X:ROI_END_X] = segment_roi
    
    return segment_original, keypoint_in_original

print("=== PyTorch interpolate实现 ===")
torch_segment, torch_keypoint = process_with_pytorch(original_img)
print(f"检测到的关键点坐标: {torch_keypoint}")
print(f"分割区域像素数: {np.sum(torch_segment)}")

# 立即显示 PyTorch 结果
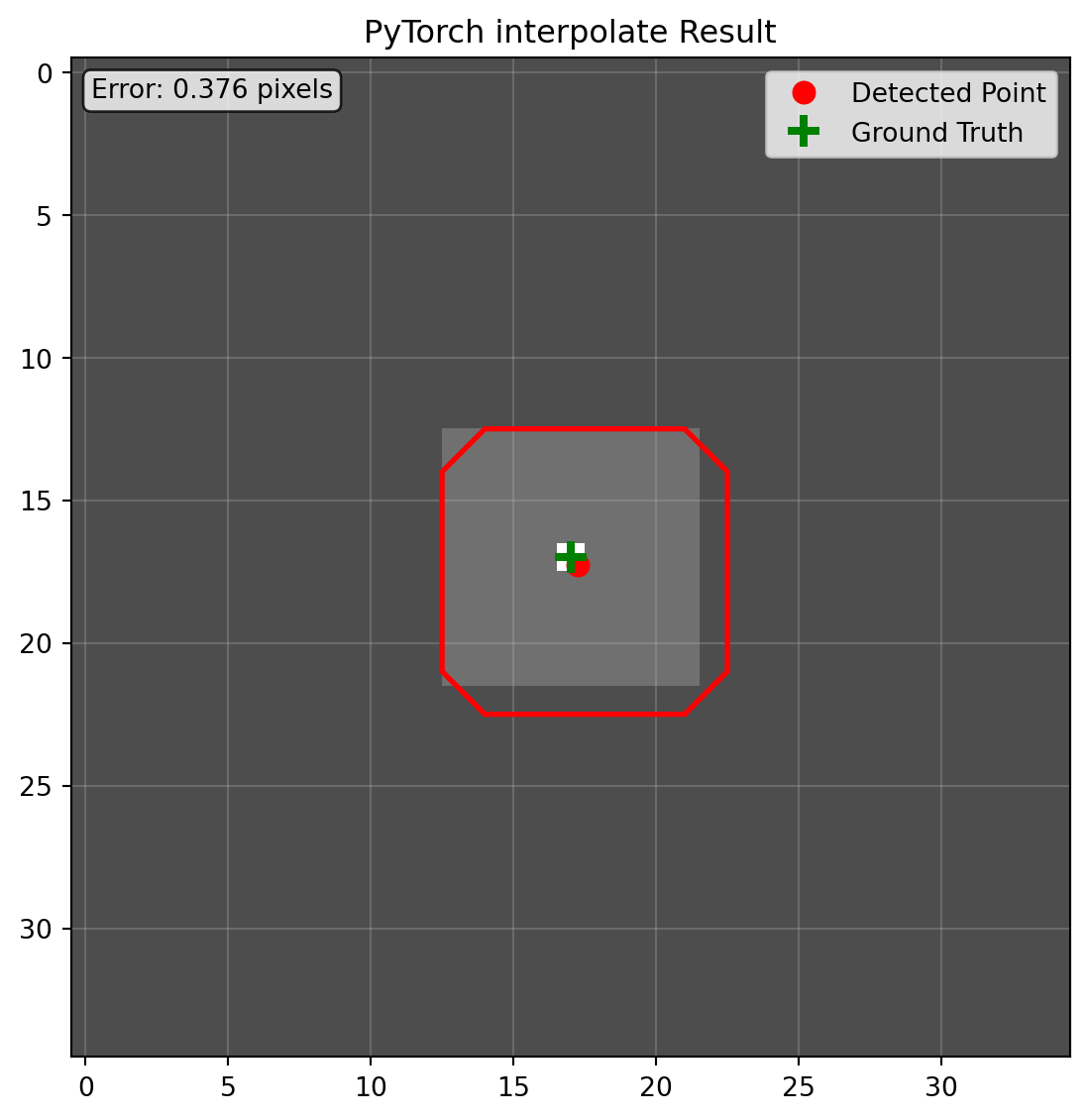
plot_result(original_img, torch_segment, torch_keypoint, "PyTorch interpolate", true_keypoint)

PyTorch interpolate 的问题分析：

• align_corners 混淆：True/False 产生不同坐标映射公式，易出错
• 维度管理冗余：需手动添加/移除 batch、channel 维度
• 最近邻偏移：可见预测的 mask 与原图存在偏移

方法四：SpaceTransformer 实现

from spacetransformer.core import Space
from spacetransformer.torch import warp_image
from spacetransformer.core import warp_point
import torch

def process_with_spacetransformer(img):
    """使用 SpaceTransformer 实现流水线"""
    
    # 定义原始图像空间
    original_space = Space(
        shape=[1]+list(img.shape),
        spacing=(1.0, 1.0, 1.0),
        origin=(0.0, 0.0, 0.0)
    )
    
    # 声明式定义目标空间：ROI 提取 + 重采样（使用全局参数）
    target_space = (original_space
        .apply_bbox([(0,1), (ROI_START_Y, ROI_END_Y), (ROI_START_X, ROI_END_X)])  # 偏移ROI
        .apply_shape((1, TARGET_SIZE, TARGET_SIZE))             # 重采样到目标尺寸
    )
    
    # 执行变换
    resampled_img = warp_image(img[None], original_space, target_space, 
                                mode='trilinear', pad_value=0, cuda_device='cpu',
                                numpy=True)[0]
    
    # 分析处理
    segment_result = get_segmentation(resampled_img)
    keypoint_2d = get_keypoint(resampled_img)
    
    # 将 2D 关键点转换为 3D 格式 (z=0, y, x) 供 SpaceTransformer 使用
    keypoint_3d = np.array([[0, keypoint_2d[0], keypoint_2d[1]]])  # shape: (1, 3)
    # 结果回传：一行代码完成逆变换
    segment_original = warp_image(segment_result[None],     target_space, original_space,
                                       mode='nearest', pad_value=0, cuda_device='cpu',numpy=True)[0]
    keypoint_3d_original = warp_point(keypoint_3d, target_space, original_space)[0]
    
    # 转换回2D格式 (y, x)
    keypoint_original = keypoint_3d_original[0, 1:3]  
    
    return segment_original, keypoint_original

print("=== SpaceTransformer实现 ===")
st_segment, st_keypoint = process_with_spacetransformer(original_img)
print(f"检测到的关键点坐标: {st_keypoint}")
print(f"分割区域像素数: {np.sum(st_segment)}")

# 立即显示 SpaceTransformer 结果
plot_result(original_img, st_segment, st_keypoint, "SpaceTransformer", true_keypoint)

实验结果分析与总结

通过上述对比实验，我们可以清晰地观察到各个库在空间变换精度和实现复杂度方面的显著差异：

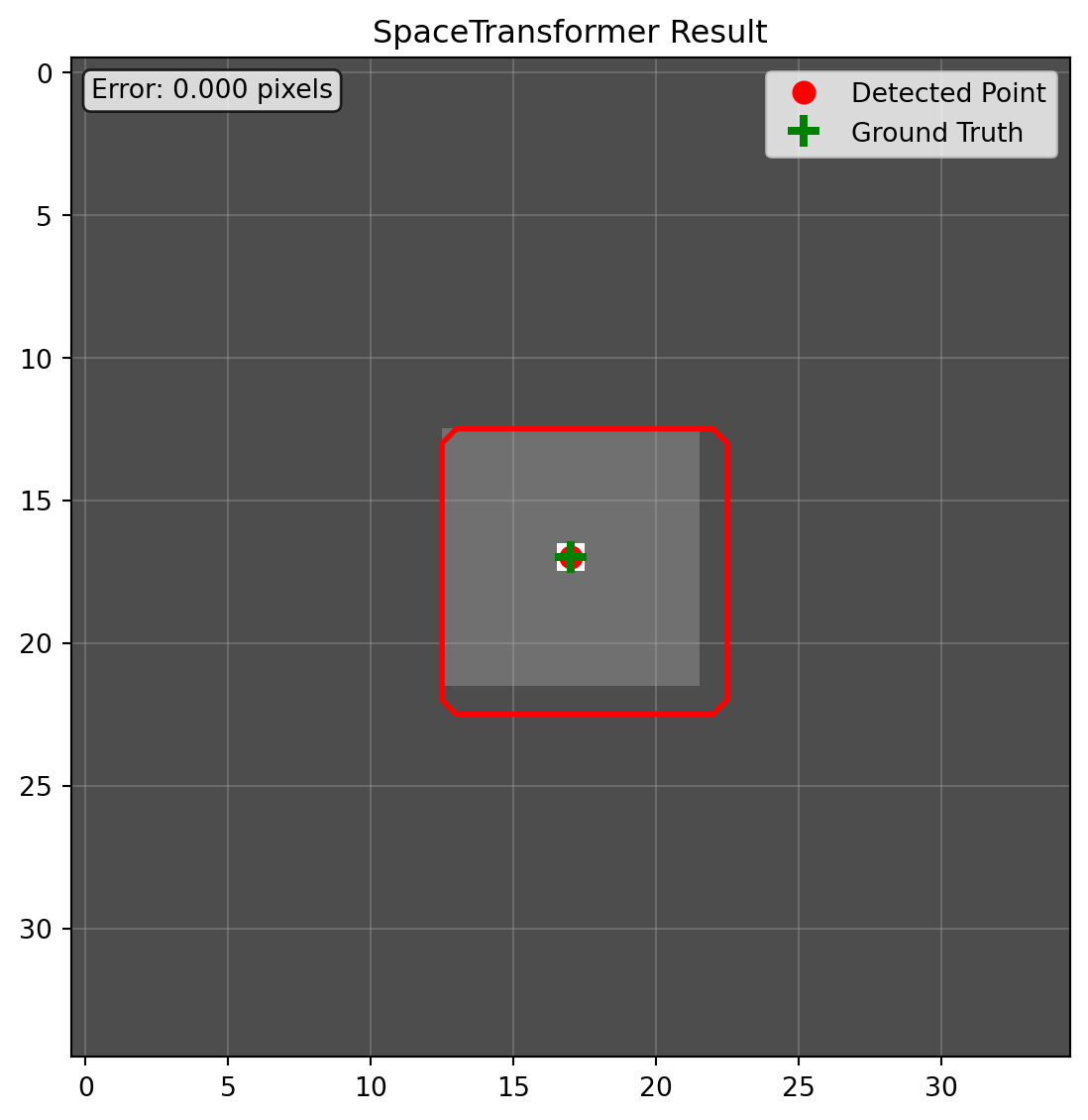
精度对比：除 SpaceTransformer 外，其他主流库均存在不同程度的坐标偏移。其中 PyTorch 的实现甚至出现明显的分割掩膜偏移，医学场景下可能导致严重后果。SpaceTransformer 通过精确空间描述，有效避免这类损失。

开发效率对比：从代码复杂度看，SpaceTransformer 优势明显。传统方法需手动管理坐标变换链、参数配置与维度处理，并针对不同元素维持不同变换；SpaceTransformer 以声明式空间定义与自动化计算，将几十行实现收敛为少量核心逻辑，显著提升可维护性。

架构设计优势：SpaceTransformer 采用“计算逻辑与业务逻辑分离”，封装复杂、易错的底层计算，使空间变换对用户透明，开发者可专注算法而非坐标细节。

在接下来的章节中，我们将分析问题根源，阐述 SpaceTransformer 的设计原理与技术实现，帮助读者理解其在医学图像空间变换中的优势。